

The Laplace Transform of standard functions can be used to efficiently solve complex equations.
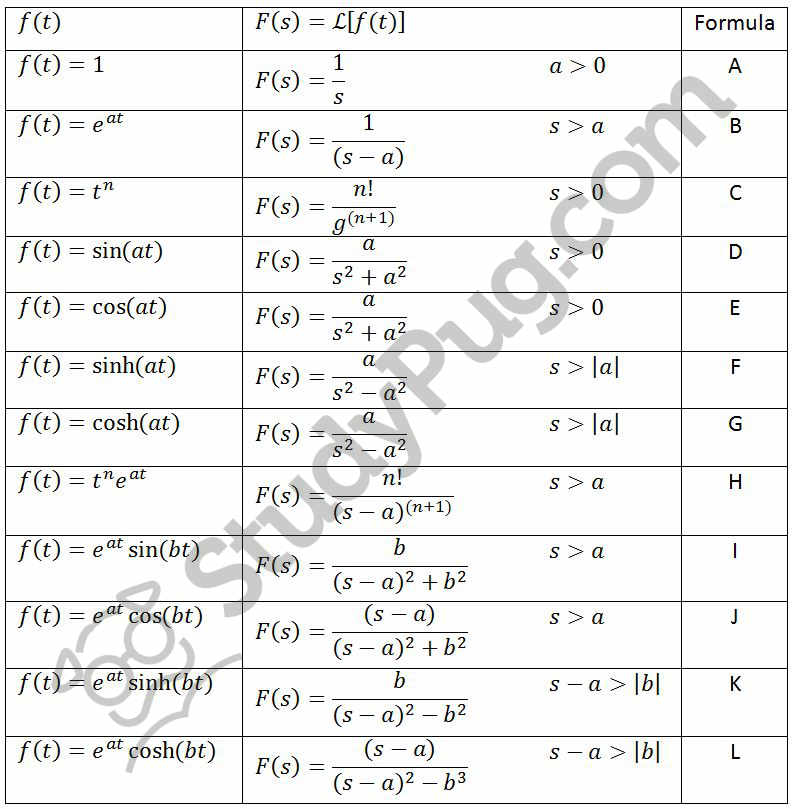
These are some basic concepts involving the Laplace Transform, there are a lot of things that are to be discussed, and we may have a further emphasis in our lectures. If F(s) is the Laplace transform of the causal signal f(t), and H(s) is Laplace transform of its impulse response, then the Laplace transform of the convolution integral of 𝑓(𝑡) with ℎ(𝑡) is If f(t) is a function of time that is defined for all values of ‘t’, then Laplace transform of 𝑓(𝑡) denoted by ℒ=𝑒 −𝑎𝑠𝐹(𝑠) Property of Convolution Integral s 29-37 ODEs AND SYSTEMS LAPLACE TRANSFORMS Find the transform, indicating the method used and showing Solve by the Laplace transform, showing the details and graphing the solution: 29. In simple words, the Laplace Transform will function as a translator for the foreign tourist. To make this simple we convert these complex time-domain equations into the frequency domain where they will be simply solvable algebraic functions. Every time it is not feasible to solve them in the time domain, especially the differential equations. To facilitate the design and simulation we must go through various mathematical equations. In engineering, simulation, and design are the crucial stages in the physical realization of any invention because one cannot afford the trial-and-error method on a complex engineering project. The laplace calculator will shows the results as: First and foremost, the calculator displays. This is true when s is greater than a, or a is less than s. The Laplace transform of e to the at is equal to 1/(s-a) as long as we make the assumption that s is greater than a. So we have our next entry in our Laplace transform table. Step 3: To acquire the integral transformation, click the 'Calculate' button. And thats just the same thing as 1/(s-a). Step 2: Click on to 'Load Example' to calculate any other example (Optional). The Laplace Transform is a useful tool for analyzing any electrical circuit, which we can convert from the Integral-Differential Equations to Algebraic Equations by replacing the original variables with new ones representing their Integral and Derivative counterpart. Step 1: In the input field, type the function, function variable, and transformation variable.


 0 kommentar(er)
0 kommentar(er)
